Mathematics, Your Ally for Better Prototyping
How to put variables and formulas to your advantage for more dynamic prototypes in ProtoPie


Realistic prototypes are on every designer’s wishlist. However, more often than not, designers find themselves with some difficulties in how to take their prototypes to the next level. The truth is that creating dynamic and realistic prototypes can become an easier task with some knowledge and practices in mathematics. Actually, I am not referring to pure mathematics as you learned it at school, but closer to the arts or techniques based on the calculation of numbers, acquiring a more mathematical way of thinking.
I will go through this topic with a step-by-step approach giving you some tips on using variables and formulas in ProtoPie.
Variables and formulas you say?
These are ProtoPie its unique features that unlock the potential of interactions, making them far more dynamic and realistic. The beauty of these features is that you can define your own variables and create your own formulas where you can use arithmetic operations, variables, and functions. Basically, giving you unlimited possibilities to create anything you want.
Let’s get started with some examples.
Slider
You can easily build a slider using the Drag trigger and Scale response. You can drag the edge of the slider and adjust its height.
You, surely, want to see what percentages it reaches or the percentile changes while dragging the slider. In many cases, the slider doesn’t exactly have a height of 100 px or a height that would match the percentages 1:1. So, you’ll need some math to make this work. Let’s look into this proportional expression.
Current Percentage = (100% × Current Height) ÷ Slider’s HeightFor example, if you drag 40 pixels out of the 530-pixel height slider, you reached a percentage of 7.547%. Super easy, right? Here, you can use some functions for displaying the percentage values better:
- ceil: Round up to the first decimal place. e.g., ceil(7.547) = 8
- round: Round to the first decimal place. e.g., round(7.547) = 8
- floor: Round down to the first decimal place. e.g., floor(7.547) = 7
Finally, you can try the following formula for the percentage presentation.
Current Percentage = floor{(100% × Current Height) ÷ Slider’s Height}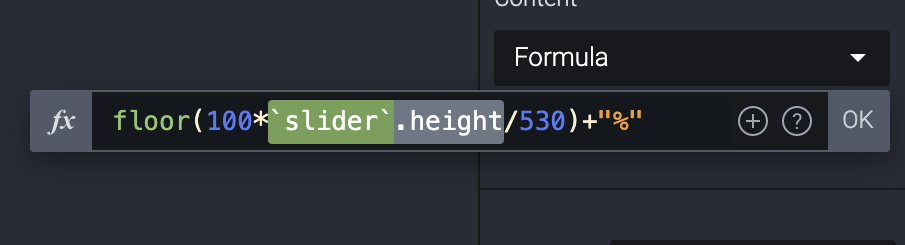
Distance display
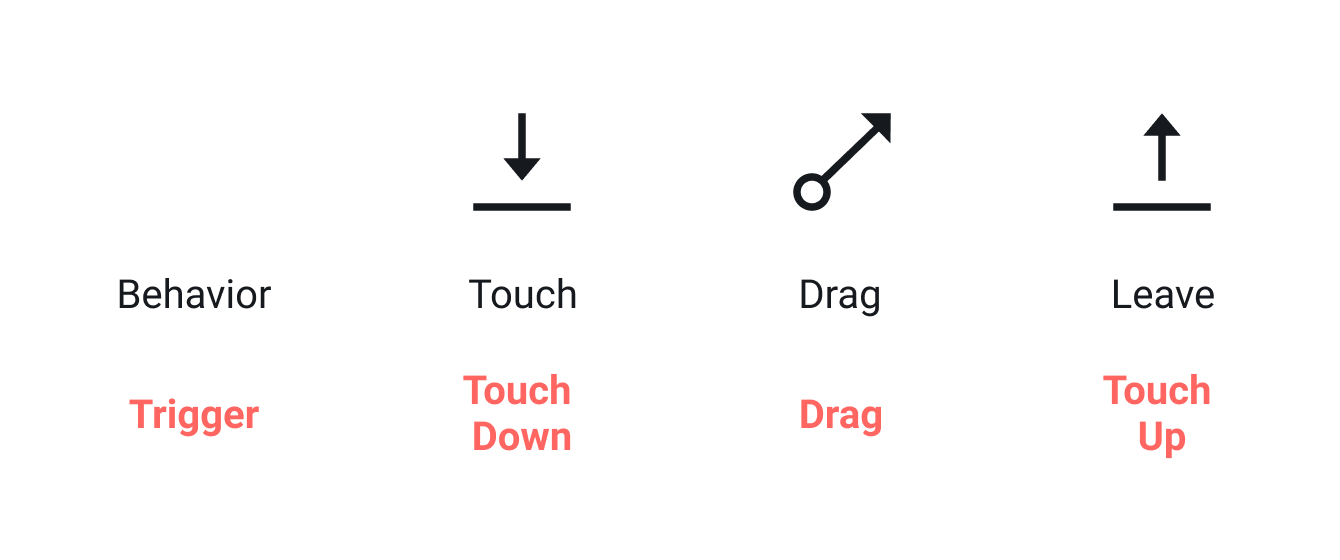
Imagine a circle on a touchscreen and you want to know the drag distance. Of course, it is relatively easy to get the distance as long as you see the Y positions at the departure and destination point after dragging it. But then, how to get those values? You need to look into the dragging behavior to solve this problem. Your fingerpad touches the screen and initiates dragging, and leaves after dragging. So, I would say that you touch the screen at the departure point and leave at the destination point. Voila!
Check out the Distance Pie File
You need to understand the difference between Touch Up and Touch Down triggers. Also, you need two variables. Assign the Y position of the circle to the first variable when you touch down the touchscreen and assign it to the second variable when you touch up. You can determine the difference between the two variables, which comes down to the drag distance.
Distance = the second variable − the first variableThe positive distance value means moving downward and the negative one means upward. If you want to show just distance value without a minus symbol, you can use the abs function.
abs(-135.6) = 135.6Swipe counter
What if you don’t have a visible controller on display but want to know the distance dragged? For example, you might want to set up the room's temperate with an eyes-free user interface on the smartphone. Sounds too complicated? Here is a simple solution: ProtoPie has a handful of predefined variables.
- $touchY: Y position of the touchpoint
- $touchVelocityY: distance to move during a unit time and direction
Touch Velocity shows the direction as well as speed, which is a distance per time. It shows a positive value when you drag downward and a negative value for upward. Yes, you’re almost done.
Lastly, you can make a counter and increase the counter every time you drag a certain distance upward and decrease when dragging downward.
Knob counter
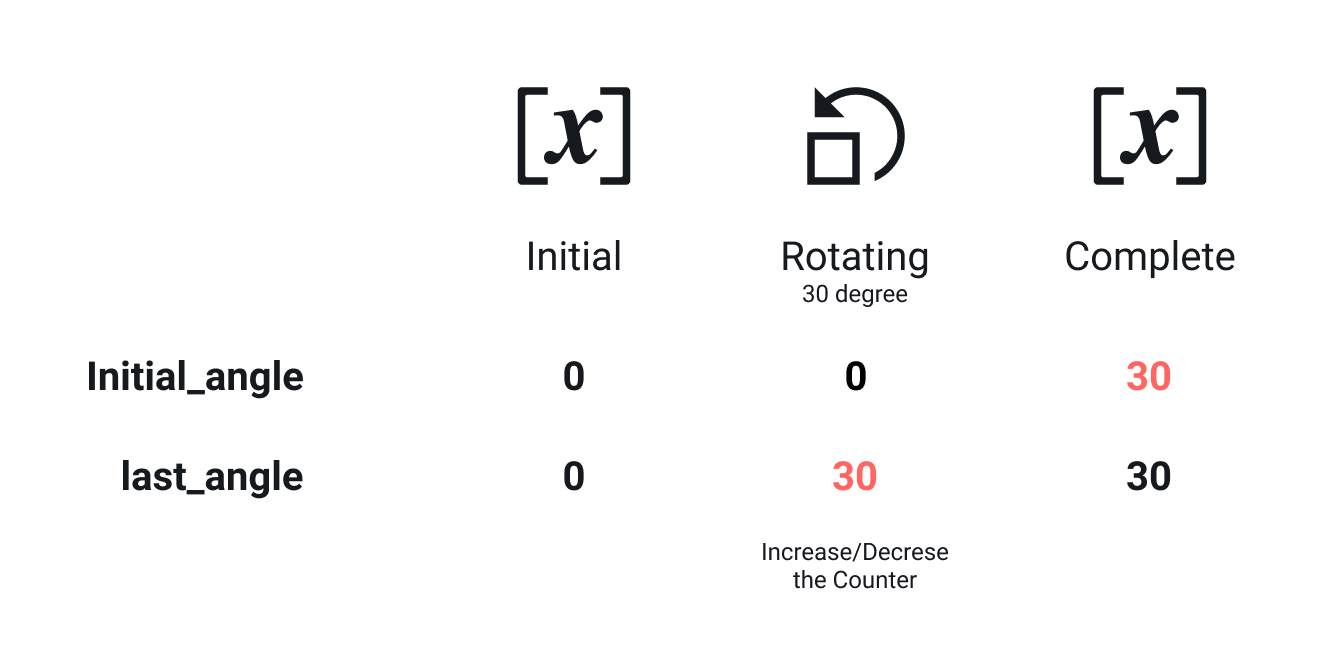
Many knobs work with a certain rotation amount rather than a specific angle. Think of a knob to adjust the temperature on the center display in the car.
You need two variables to assign the initial angle and last angle while rotating the knob. A positive value of difference means you rotate clockwise, and a negative one means counterclockwise. In this example, it is important to update the initial angle variable to the last angle after increasing or decreasing the counter for the next calculation.
Timer
Digital assistants or appliances have timers to set the time for notification purposes or completed tasks.
You can make a timer in the same way as the counters. However, we see the clock format's timer, usually like 1:30 (1 hour and a half) rather than 90 minutes. All right, let’s go back to school and look into divisions. If you divide 90 by 60, the quotient is 1 with a remainder of 30.
90 ÷ 60 = 60 × 1 + 30You can explain it with the following expression as well.
90 ÷ 60 = 1 R 30The Mod (Modulo) operation helps you to get reminders like the following.
90 mod 60 = 30
90 % 60 = 30So, you can convert Counter to Timer format using division and mod operations.
Hour = floor(Counter / 60)
Minute = Counter % 60One more thing, you might want to show two digits always for minutes like “05” minutes. You can use lpad function to add “0” to the left side of the number in order to have 2 digits. lpad (5, 2, “0”) returns “05”.
lpad(Counter % 60, 2, "0")Here some examples of what you can achieve by applying some of the techniques I showed you today!
I have listed some techniques and tips based on mathematics. You certainly don’t have to be a rocket scientist or mathematician. As long as you can free your ideas and explain them in the right way, that would be plenty already. If you have any more tips not listed here, please leave them in the comments.


